Solving cubic polynomials: Difference between revisions
| Line 72: | Line 72: | ||
== Case of positive determinant <math>\Delta>0</math> == | == Case of positive determinant <math>\Delta>0</math> == | ||
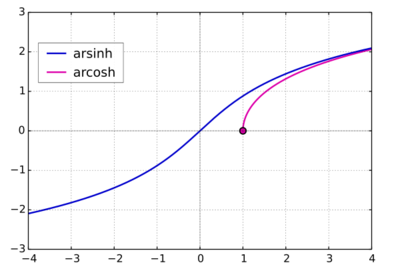
When <math>\Delta = Q^2 - P^3 > 0</math>, we can no longer infer that <math>P > 0</math>, and the complex domain is less helpful. The solution arises from the use of two 'triple angle' hyperbolic trigonometric identities: | When <math>\Delta = Q^2 - P^3 > 0</math>, we can no longer infer that <math>P > 0</math>, and the complex domain is less helpful. The solution arises from the use of two 'triple angle' hyperbolic trigonometric identities:[[Image:InverseHypTrig.png|thumb|400px|Inverse hyperbolic trignometric functions]] | ||
:<math>\cosh 3\theta = 4 \cosh^3 \theta - 3 \cosh \theta</math> | :<math>\cosh 3\theta = 4 \cosh^3 \theta - 3 \cosh \theta</math> | ||
:<math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta</math> | :<math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta</math> | ||
We would like to get our depressed polynomial <math>y^3 - 3Py - 2Q = 0</math> into a form similar to either of the above. We can substitute <math>y = u~\mathrm{hyp}\left(\theta\right)</math> to obtain: | We would like to get our depressed polynomial <math>y^3 - 3Py - 2Q = 0</math> into a form similar to either of the above. We can substitute <math>y = u~\mathrm{hyp}\left(\theta\right)</math> (where <math>\mathrm{hyp}</math> is an unspecified hyperbolic trigonometric function) to obtain: | ||
:<math>u^3~\mathrm{hyp}^3\left(\theta\right) - 3 P u~\mathrm{hyp}\left(\theta\right) - 2 Q = 0</math> | :<math>u^3~\mathrm{hyp}^3\left(\theta\right) - 3 P u~\mathrm{hyp}\left(\theta\right) - 2 Q = 0</math> | ||
| Line 90: | Line 90: | ||
:<math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta = \frac{8Q}{u^3}</math> (for <math>P<0</math>). | :<math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta = \frac{8Q}{u^3}</math> (for <math>P<0</math>). | ||
There are no problems with the <math>P<0</math> case, because <math>\sinh^{-1}</math> is always defined, and with <math>u=2\sqrt{\left|P\right|}</math>, we get <math>\frac{8Q}{u^3} = \frac{Q}{\sqrt{\left|P\right|^3}}</math>. | |||
However, for the <math>P>0</math> case, <math>\cosh^{-1}</math> will only be defined when <math>\frac{8Q}{u^3}\ge 1</math>. We carefully choose <math>u = 2\sqrt{\left|P\right|}\sgn{Q}</math>, which means that our condition is | |||
:<math>\frac{8Q}{u^3} = \frac{8 \left|Q\right| \sgn{Q}}{4P \cdot 2\sqrt{\left|P\right|}\sgn{Q}} = \frac{\left|Q\right|}{\sqrt{\left|P\right|^3}} \ge 1</math> | |||
Given that <math>\Delta = Q^2-P^3 > 0</math> and <math>P>0</math>, hence <math>\left|Q\right| > \sqrt{\left|P\right|^3}</math>, we can see that this condition is always satisfied with the chosen <math>u</math>. | |||
The overall result for <math>\Delta > 0</math> can then be written, using that <math>\left|Q\right| = Q \sgn{Q}</math>: | |||
:<math>y = 2S\sqrt{\left|P\right|}~\mathrm{hyp}\left(\frac{1}{3}~\mathrm{hyp}^{-1} \frac{QS}{\sqrt{\left|P\right|^3}}\right) | |||
\text{ where } | |||
\begin{cases} | |||
\text{if }P>0 \text{,}& \mathrm{hyp}=\cosh\text{ and } S = 1 \\ | |||
\text{if }P<0 \text{,}& \mathrm{hyp}=\sinh\text{ and } S = \sgn{Q} | |||
\end{cases} | |||
</math> | |||
The case <math>P=0</math> was already handled earlier. | |||
== Calculation checking == | == Calculation checking == | ||
Revision as of 08:43, 2 July 2022
There are many sources for how to solve cubic polynomials, often with many peripheral details, so a summarised and simplfied version is helpful when implementing a new code. This page is an attempt to record that.
General solution
We will consider the monic cubic polynomial in <math>x</math>, with <math>a</math>, <math>b</math> and <math>c</math> real-valued:
- <math> x^3 + a x^2 + b x + c = 0 </math>
To solve for <math>x</math>, we first calculate the coefficients of an equivalent 'depressed cubic' <math>y^3 - 3P y - 2Q = 0</math>, without loss of generality, by substituting <math>x = y - a/3</math>:
- <math>3P = \frac{a^2}{3} - b</math>
- <math>2Q = \frac{2}{27} a^3 - \frac{1}{3} ab + c</math>
If <math>P</math> and <math>Q</math> are both zero, then we can stop here with a triple root at <math>y = 0</math>, which is equivalent to <math>x = -\frac{a}{3}</math>.
If only <math>P</math> is zero, then <math>y^3 = 2Q</math>, so <math>x = \sqrt[3]{2Q}-\frac{a}{3}</math>.
If only <math>Q</math> is zero, the depressed cubic is simply <math>y^3 - 3Py = y \left(y^2 - 3P \right) = 0</math>, which has a real root at <math>y=0</math> and two more at <math>y = \pm \sqrt{3P}</math>, which may be either real or imaginary, depending on the sign of <math>P</math>.
Otherwise, the depressed cubic can then be converted into a quadratic in <math>z^3</math> via the 'magic' Vieta substitution <math>y = z + \frac{P}{z}</math>,
- <math>\left(z^3\right)^2 - 2Q \left(z^3\right) + P^3 = 0</math>
for which the solution is
- <math>z^3 = Q \pm \sqrt{Q^2 - P^3}</math>(1)
The original cubics (in <math>x</math> and <math>y</math>) have real coefficients, which means that any complex roots must appear with their complex conjugate. As such, the cubic equations must have either one or three real roots, and two or zero complex roots. The determinant <math>\Delta = Q^2 - P^3</math> is critical in determining which case arises. (Note that the discriminant can also be arrived at via another path with the same result.)
Case of negative determinant <math>\Delta<0</math>
If <math>\Delta = Q^2 - P^3 < 0</math> then <math>P^3</math> and hence <math>P</math> must be positive, and we must enter the complex domain to solve
- <math>z^3 = R</math> or <math>z^3 = \overline{R}</math>
where, using <math>\sqrt{\Delta}=-i\sqrt{-\Delta}</math>,
- <math>R = Q \pm i \sqrt{P^3 - Q^2}</math>
or equivalently,
- <math>\left|R\right| = \sqrt{Q^2 + P^3 - Q^2} = \sqrt{P^3} </math>
- <math>\arg R = \pm\theta</math>, where
- <math>\theta = \cos^{-1} \left(\frac{Q}{\sqrt{P^3}}\right)</math>.
The solution for <math>z</math> is then
- <math>z = \sqrt{P} \exp \left(i \frac{\pm \theta + 2\pi k}{3}\right)</math> where <math>k \in \left\lbrace 0,1,2 \right\rbrace</math>, for <math>z^3 = R</math>
There are six values for <math>z</math> here, arising from combining the three roots <math>k \in \left\lbrace 0,1,2 \right\rbrace</math> and the <math>\pm</math> cases for <math>\theta</math>.
Using these values of <math>z</math>, we can now evaluate the solutions <math>y</math> of the depressed cubic, via <math>y = z + \frac{P}{z}</math>. Here, we make use of the facts that <math>\frac{1}{r e^{i\theta}} = \frac{1}{r} e^{-i\theta}</math> and <math>e^{i\phi}+e^{-i\phi}=2\cos\phi</math>
- <math>
\begin{alignat}{2} y &= \sqrt{P} \exp \left(i \frac{\pm \theta + 2\pi k}{3}\right) + \frac{P}{\sqrt{P} \exp \left(i \frac{\pm \theta + 2\pi k}{3}\right)} \\ &= \sqrt{P} \exp \left(i \frac{\pm \theta + 2\pi k}{3}\right) + \sqrt{P} \exp \left(-i \frac{\pm \theta + 2\pi k}{3}\right) \\ &= 2\sqrt{P} \cos \left(\frac{\pm \theta + 2\pi k}{3}\right) \end{alignat} </math>
It can readily be seen that the six solutions have reduced to three, because <math>\cos\left(-\phi\right)=\cos\phi</math> and <math>\cos\left(\phi+2\pi\right)=\cos\phi</math>, and also that all of the solutions are real. We can drop the <math>\pm</math>, therefore, and write:
- <math>y = 2\sqrt{P} \cos \left(\frac{\theta + 2\pi k}{3}\right)</math>, with <math>k \in \left\lbrace 0,1,2 \right\rbrace</math>,
Finally, subsituting for <math>x</math>:
- <math>x = -\frac{a}{3} + 2\sqrt{P} \cos \left(\frac{\theta + 2\pi k}{3}\right)</math>, with <math>k \in \left\lbrace 0,1,2 \right\rbrace</math>.
After allowing for differences in notation, this solution can be seen to be identical to the one obtained via use of the cosine triple-angle identity.
Case of positive determinant <math>\Delta>0</math>
When <math>\Delta = Q^2 - P^3 > 0</math>, we can no longer infer that <math>P > 0</math>, and the complex domain is less helpful. The solution arises from the use of two 'triple angle' hyperbolic trigonometric identities:
- <math>\cosh 3\theta = 4 \cosh^3 \theta - 3 \cosh \theta</math>
- <math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta</math>
We would like to get our depressed polynomial <math>y^3 - 3Py - 2Q = 0</math> into a form similar to either of the above. We can substitute <math>y = u~\mathrm{hyp}\left(\theta\right)</math> (where <math>\mathrm{hyp}</math> is an unspecified hyperbolic trigonometric function) to obtain:
- <math>u^3~\mathrm{hyp}^3\left(\theta\right) - 3 P u~\mathrm{hyp}\left(\theta\right) - 2 Q = 0</math>
Then multiply the equation by <math>4/u^3</math> (requiring that <math>u \ne 0</math>):
- <math>4 \mathrm{hyp}^3\left(\theta\right) - 3 \frac{4P}{u^2} \mathrm{hyp}\left(\theta\right) - \frac{8Q}{u^3} = 0</math>
Now, if <math>P > 0</math>, we can require that <math>\frac{4P}{u^2} = 1</math> and use <math>\mathrm{hyp}=\cosh</math>. Or, if <math>P < 0</math>, we can require that <math>\frac{4P}{u^2} = -1</math> and <math>\mathrm{hyp}=\sinh</math>. Together,
- <math>\cosh 3\theta = 4 \cosh^3 \theta - 3 \cosh \theta = \frac{8Q}{u^3} \text{ (for }P>0\text{), or}</math>
- <math>\sinh 3\theta = 4 \sinh^3 \theta + 3 \sinh \theta = \frac{8Q}{u^3}</math> (for <math>P<0</math>).
There are no problems with the <math>P<0</math> case, because <math>\sinh^{-1}</math> is always defined, and with <math>u=2\sqrt{\left|P\right|}</math>, we get <math>\frac{8Q}{u^3} = \frac{Q}{\sqrt{\left|P\right|^3}}</math>.
However, for the <math>P>0</math> case, <math>\cosh^{-1}</math> will only be defined when <math>\frac{8Q}{u^3}\ge 1</math>. We carefully choose <math>u = 2\sqrt{\left|P\right|}\sgn{Q}</math>, which means that our condition is
- <math>\frac{8Q}{u^3} = \frac{8 \left|Q\right| \sgn{Q}}{4P \cdot 2\sqrt{\left|P\right|}\sgn{Q}} = \frac{\left|Q\right|}{\sqrt{\left|P\right|^3}} \ge 1</math>
Given that <math>\Delta = Q^2-P^3 > 0</math> and <math>P>0</math>, hence <math>\left|Q\right| > \sqrt{\left|P\right|^3}</math>, we can see that this condition is always satisfied with the chosen <math>u</math>.
The overall result for <math>\Delta > 0</math> can then be written, using that <math>\left|Q\right| = Q \sgn{Q}</math>:
- <math>y = 2S\sqrt{\left|P\right|}~\mathrm{hyp}\left(\frac{1}{3}~\mathrm{hyp}^{-1} \frac{QS}{\sqrt{\left|P\right|^3}}\right)
\text{ where } \begin{cases} \text{if }P>0 \text{,}& \mathrm{hyp}=\cosh\text{ and } S = 1 \\ \text{if }P<0 \text{,}& \mathrm{hyp}=\sinh\text{ and } S = \sgn{Q} \end{cases} </math>
The case <math>P=0</math> was already handled earlier.
Calculation checking
The following sympy code can be used to confirm the above results:
Invalid language.
You need to specify a language like this: <source lang="html">...</source>
Supported languages for syntax highlighting:
a4c, abap, abc, abnf, actionscript, ada, agda, alan, algol, ampl, amtrix, applescript, arc, arm, as400cl, ascend, asciidoc, asp, aspect, assembler, ats, autohotkey, autoit, avenue, awk, ballerina, bat, bbcode, bcpl, bibtex, biferno, bison, blitzbasic, bms, bnf, boo, c, carbon, ceylon, charmm, chill, chpl, clean, clearbasic, clipper, clojure, clp, cmake, cobol, coffeescript, coldfusion, conf, cpp2, critic, crk, crystal, cs_block_regex, csharp, css, d, dart, delphi, diff, dockerfile, dts, dylan, ebnf, ebnf2, eiffel, elixir, elm, email, erb, erlang, euphoria, exapunks, excel, express, factor, fame, fasm, felix, fish, fortran77, fortran90, frink, fsharp, fstab, fx, gambas, gdb, gdscript, go, graphviz, haml, hare, haskell, haxe, hcl, html, httpd, hugo, icon, idl, idlang, inc_luatex, informix, ini, innosetup, interlis, io, jam, jasmin, java, javascript, js_regex, json, jsp, jsx, julia, kotlin, ldif, less, lhs, lilypond, limbo, lindenscript, lisp, logtalk, lotos, lotus, lua, luban, makefile, maple, markdown, matlab, maya, mercury, meson, miranda, mod2, mod3, modelica, moon, ms, msl, mssql, mxml, n3, nasal, nbc, nemerle, netrexx, nginx, nice, nim, nix, nsis, nxc, oberon, objc, ocaml, octave, oorexx, org, os, oz, paradox, pas, pdf, perl, php, pike, pl1, plperl, plpython, pltcl, po, polygen, pony, pov, powershell, pro, progress, ps, psl, pure, purebasic, purescript, pyrex, python, q, qmake, qml, qu, r, rebol, rego, rexx, rnc, rpg, rpl, rst, ruby, rust, s, sam, sas, scad, scala, scilab, scss, shellscript, slim, small, smalltalk, sml, snmp, snobol, solidity, spec, spn, sql, squirrel, styl, svg, swift, sybase, tcl, tcsh, terraform, tex, toml, tsql, tsx, ttcn3, txt, typescript, upc, vala, vb, verilog, vhd, vimscript, vue, wat, whiley, wren, xml, xpp, yaiff, yaml, yaml_ansible, yang, zig, znn