User:Sidharth: Difference between revisions
| Line 178: | Line 178: | ||
{| class="wikitable" style="text-align: center" | {| class="wikitable" style="text-align: center" | ||
|+ '''Comparing % Error for the | |+ '''Comparing Average % Error for the five variables''' | ||
|- | |- | ||
! | ! | ||
| Line 185: | Line 185: | ||
|- | |- | ||
|Pressure | |Pressure | ||
| | |0.001419 | ||
| | | | ||
|- | |- | ||
|Enthalpy | |Enthalpy | ||
| | |0.000892 | ||
| | | | ||
|- | |- | ||
|Entropy | |Entropy | ||
| | |0.024706 | ||
| | | | ||
|- | |- | ||
|Internal Energy | |Internal Energy | ||
| | |0.005294 | ||
| | | | ||
|- | |- | ||
|Gibb's Energy | |Gibb's Energy | ||
| | |0.082597 | ||
| | | | ||
|} | |} | ||
Revision as of 01:48, 1 July 2015
Tabulated frontend to FPROPS
Theory
We intend to implement a tabulated frontend to the existing FPROPS. The main idea for this comes from the Tabulated Taylor Series Expansion (TTSE) approach. We would make a 2 dimensional grid in temperature and mass density <math> (T,\rho) </math>. The essence of the approach is that if we know the value of a thermodynamic property <math> X </math> and its first, second and mixed derivative terms with respect to two independent variables <math> (T,\rho) </math> at a certain point <math> (T_i,\rho_j) </math> then we can compute the value of the function at a small distance from the point by the following Taylor series expansion.
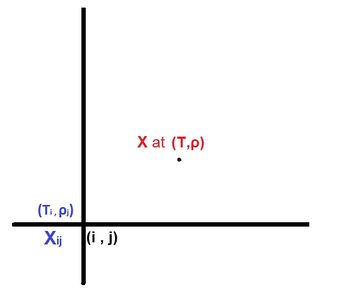
<math> X = X_{i,j} + (T-T_i) \frac{\partial X}{\partial T}\bigg|_{i,j} + \frac{1}{2} (T-T_i)^2 \frac{\partial^2 X}{\partial T^2}\bigg|_{i,j} + (\rho-\rho_j) \frac{\partial X}{\partial \rho}\bigg|_{i,j} + \frac{1}{2} (\rho-\rho_j)^2 \frac{\partial^2 X}{\partial \rho^2}\bigg|_{i,j} + (T-T_i) (\rho-\rho_j) \frac{\partial^2 X}{\partial T \partial \rho}\bigg|_{i,j} </math>
Here X could be thermodynamic properties like pressure, enthalpy etc. For implementing this we can allocate <math> (200 X 200) </math> grid with each of the six terms in the above equation for the key state properties we need, namely <math> (Pressure , Enthalpy, Entropy) </math>. In order to do this, the backend's (Helmholtz, Pengrob) need to be supplemented with additional routines, to compute the first and second order derivatives. For instance for entropy expansion we need
<math>
\frac{\partial s}{\partial T}\bigg|_{\rho} , \frac{\partial^2 s}{\partial T^2}\bigg|_{\rho} , \frac{\partial s}{\partial \rho}\bigg|_{T} , \frac{\partial^2 s}{\partial \rho^2}\bigg|_{T} </math> and <math> \frac{\partial^2 s}{\partial \rho \partial T}
</math>
FPROPS module in ASCEND
FPROPS uses function pointers from the underlying correlation (helmholtz or Pengrob) to calculate fundamental quantities with Temperature and <math> \rho</math> as the input. Following are those functions of fprops :-
fprops_p() fprops_u() fprops_h() fprops_s() fprops_g()
fprops_dpdrho_T() fprops_alphap() fprops_betaP() fprops_a()
fprops_cp() fprops_cv() fprops_w()
Both the underlying correlations provide these 13 functions calculated from first principles, with T and <math>\rho</math> as inputs. So the TTSE implementation for a specific liquid and a specific correlation (H or P) should eventually generate tables for each of the above 13 entries. For the saturation function fprops_sat(), takes only 1 input (temperature) and returns saturated liquid density, saturated vapour density and the saturation pressure. This function involves solving equations iteratively and tabulation should speed up calculation on saturation curve.
To begin with we can tabulate the following functions:
- helmholtz_p
- helmholtz_s
- helmholtz_u
- helmholtz_g
- helmholtz_h
In order to use look up tables for TTSE method inside these routines we need to complete the set of all partial derivatives we need :-
For each of the above variable X (where X is either of P,s,u,g and h) we need <math> \frac{\partial X}{\partial T}\bigg|_{\rho} ,
\frac{\partial^2 X}{\partial T^2}\bigg|_{\rho} ,
\frac{\partial X}{\partial \rho}\bigg|_{T} ,
\frac{\partial^2 X}{\partial \rho^2}\bigg|_{T}</math> and <math>
\frac{\partial^2 X}{\partial \rho \partial T} </math>
Many of the partial derivatives are already listed in helmholtz.c. Specifically the new 18 ones we need to implement are:
| Variable | Partial derivative with T constant |
Partial derivative with <math>\rho</math> constant |
Partial second derivative with <math>\rho</math> constant |
Partial second derivative with <math>T</math> constant |
Partial mixed second derivative |
|---|---|---|---|---|---|
| Pressure, P | <already implemented> | <already implemented> | <already implemented> | helmholtz_d2pdT2_rho()
<math>\frac{\partial^2 p}{\partial (T^2)} </math> |
helmholtz_d2pdrhodT()
<math>\frac{\partial^2 p}{\partial (T \rho)} </math> |
| Enthalpy, h | <already implemented> | <already implemented> | helmholtz_d2hdrho2_T()
<math>\frac{\partial^2 h}{\partial \rho^2}\bigg|_{T}</math> |
helmholtz_d2hdT2_rho()
<math>\frac{\partial^2 h}{\partial T ^2}\bigg|_{\rho}</math> |
helmholtz_d2hdrhodT()
<math>\frac{\partial^2 h}{\partial (T \rho)} </math> |
| Internal Energy, u | <already implemented> | <already implemented> | helmholtz_d2udrho2_T()
<math>\frac{\partial^2 u}{\partial \rho^2}\bigg|_{T}</math> |
helmholtz_d2udT2_rho()
<math>\frac{\partial^2 u}{\partial T^2}\bigg|_{\rho}</math> |
helmholtz_d2udrhodT()
<math>\frac{\partial^2 u}{\partial (T \rho)}</math> |
| Entropy, s | helmholtz_dsdT_rho()
<math>\frac{\partial s}{\partial T}\bigg|_{\rho}</math> |
helmholtz_dsdrho_T()
<math>\frac{\partial s}{\partial \rho}\bigg|_{T}</math> |
helmholtz_d2sdrho2_T()
<math>\frac{\partial^2 s}{\partial \rho^2}\bigg|_{T}</math> |
helmholtz_d2sdT2_rho()
<math>\frac{\partial^2 s}{\partial T^2}\bigg|_{\rho}</math> |
helmholtz_d2sdrhodT()
<math>\frac{\partial^2 s}{\partial (T \rho)}</math> |
| Gibbs Free Energy, g | helmholtz_dgdT_rho()
<math>\frac{\partial g}{\partial T}\bigg|_{\rho}</math> |
helmholtz_dgdrho_T()
<math>\frac{\partial g}{\partial \rho}\bigg|_{T}</math> |
helmholtz_d2gdrho2_T()
<math>\frac{\partial^2 g}{\partial \rho^2}\bigg|_{T}</math> |
helmholtz_d2gdT2_rho()
<math>\frac{\partial^2 g}{\partial T^2}\bigg|_{\rho}</math> |
helmholtz_d2gdrhodT()
<math>\frac{\partial^2 g}{\partial (T \rho)}</math> |
To evaluate these drivatives we need the underlying partial derivatives of the residual and the ideal part of helmholtz function. So the three new functions needed in helmholtz.c and cp0.c
Third partial derivative of ideal part of helmholtz (all other partial derivatives invloving delta are zero) in file cp0.c
- ideal_phi_tautautau()
Third derivative of helmholtz residual function, with respect to delta once and tau twice
- helm_resid_deltautau()
Third derivative of helmholtz residual function, with respect to delta twice and tau once
- helm_resid_deldeltau()
Third derivative of helmholtz residual function, with respect to tau thrice
- helm_resid_tautautau()
Preliminary Results
In this test the fluid of choice was taken to be water. We need boundaries for the table implementation in <math>(T,\rho)</math> plane. So for this test <math> (T_{min}, T_{max}) </math> was taken to be <math> (200,4200) \quad K</math> and <math> (\rho_{min}, \rho_{max}) </math> taken to be <math> (400,4400) \quad Kg/m^3</math> . This domain was decomposed into <math> 200X200 </math> points.
The test was also done for a first order implementation of TTSE, in which we just take the below first order formulation.
<math> X = X_{i,j} + (T-T_i) \frac{\partial X}{\partial T}\bigg|_{i,j} + (\rho-\rho_j) \frac{\partial X}{\partial \rho}\bigg|_{i,j} </math>
For this particular test <math> \rho </math> was set to <math> \mathbf{200} </math> Kg/m^3 and temperature is ranged from <math> \mathbf{400}</math> Kelvins to <math> \mathbf{500} </math> Kelvins in <math> \mathbf{500} </math> equal steps. And then the five functions given below (and implemented in ttse.c) are called for the tabulated result and compared with the direct helmholtz result
evaluate_ttse_p() //for pressure
evaluate_ttse_h() //for enthalpy
evaluate_ttse_s() //for entropy
evaluate_ttse_u() //for internal energy
evaluate_ttse_g() //for Gibbs free energy
| First Order | Second Order | |
|---|---|---|
| Time In Seconds | 6.231 |
| For First Order | For Second Order | |
|---|---|---|
| Pressure | 0.001419 | |
| Enthalpy | 0.000892 | |
| Entropy | 0.024706 | |
| Internal Energy | 0.005294 | |
| Gibb's Energy | 0.082597 |
Progress Details
- Implemented all the 18 functions from Table 1 in helmholtz.c
- Implemented the above 4 functions for triple derivatives using a naive formulation from the second derivatives. Can be improved later.
- Added
struct ttsein rundata.h. This contains the necessary information needed in structure. - ttse.c and ttse.h file added to fprops/ . Here the TTSE module will be fully implemented.
- Testing module for TTSE added in test/test_ttse.c